CHAPTER 2

COMBINATORICS

“Combinatorics” is a name for the study of the methods of counting. Although one might think of counting as a simple process, it can be quite complicated if whatever we wish to count cannot readily be visualized. In combinatorics we are usually concerned not with counting physical objects, but rather with counting ways of carrying out certain procedures.

2A  Fundamental Principles

There are a few basic principles upon which much of combinatorics is based. The next few examples illustrate one of these principles.

example 1

Suppose Fritz wakes up in the morning and finds he has 3 clean pairs of pants and 4 clean shirts. How many ways can he dress for his math class? To be specific, we presume that he has a black pair of pants, a green pair, and a tan pair, while his shirts are colored lime, pink, red, and yellow. (Fritz is not a candidate for best-dressed student on campus.) We can divide the procedure of Fritz getting dressed into two “steps” - first he chooses his pants and next he chooses a shirt. If he selects black pants in the first step, then he has four ways of selecting the shirt in the second step - thus there are four ways of dressing if he wears black pants. Likewise, there are four ways of dressing if he wears green pants, and four more ways if he wears tan pants. Altogether, the number of ways he can dress then is 4 + 4 + 4 = 3 · 4 = 12.

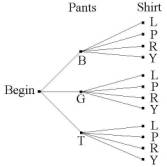The diagram at the right, a tree diagram, is a visual aid in analyzing this two-step procedure. We see that there are three ways of completing step 1, represented by the first level branches in the tree. Then for each branch in the first level, there are four second level branches, corresponding to the four ways of completing step 2. The points on the extreme right are leaves on the tree; these represent the ways of performing step 1 followed by step 2. The number of leaves is the product of the number of first level options times the number of second level options - in this case, 3 · 4 = 12.

We are now prepared to state the multiplication principle.

To keep it simple we stated the multiplication principle only for two-step procedures, but it should be clear that an analogous version applies to procedures of three or more steps. For example, suppose that Fritz has also four favorite hats, and that he must wear one of them because it is raining outside. Then we add a third step to his getting-dressed procedure - that of choosing his headwear. Now, for each of the 12 ways of completing steps 1 and 2 of getting dressed, Fritz has 4 ways of completing this third step, so the number of possibilities is multiplied by 4. His ways of getting dressed now total

If we added a fourth step - say that of choosing between 5 pairs of shoes - then we would multiply again, this time by 5, to calculate the number ways of dressing Fritz as

For procedures with several steps the tree diagram becomes more complicated, for we must add another level of branches at each step. As the numbers multiply the tree diagram might become so filled with branches that it is no longer practical to draw.

example 2

	Heads	Tails

If we flip a coin, say a penny, then the two possible outcomes are that the penny lands heads or that it lands tails. We designate these with the letters H and T.

If we flip two coins, say now a penny and a nickel, we have a two-step procedure; the first step of flipping the penny has two outcomes, as does the second step of flipping the nickel. By the multiplication principle, the number of possible outcomes in flipping two coins is 2 · 2 = 4. These four outcomes are easily listed in a table; likewise, the tree diagram for this procedure is quite simple:

Penny Nickel H H H T T H T T

As an alternative to making a table, we could simply list the four outcomes as

where the first letter in each pair refers to the penny, and the second to the nickel.

Next suppose we add a dime to the action, so that now we flip three coins. We have a 3-step procedure, and in each step there are 2 possible outcomes; thus the total number of possible outcomes in the entire procedure is 2 · 2 · 2 = 8.

Penny Nickel Dime H H H H H T H T H H T T T H H T H T T T H T T T

The outcomes may be listed in one line as

After too many coins, writing down all the outcomes becomes more trouble than it is worth; nevertheless, the multiplication principle still allows us to count their total number. For instance, the number of possible outcomes in flipping 10 coins is

example 3

How many different license plates can be made by a state, if each plate is to display three letters followed by three numbers? We divide the procedure of labeling a plate into six steps - we choose a first letter, a second, and a third, and then a first number, a second, and a third. There are 26 ways to choose a letter of the English alphabet, and there are 10 ways to choose a number from the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Thus the number of possible license plates is

(In practice there are slightly fewer possibilities, because certain combinations of letters and numbers are best avoided.)

example 4

Suppose a room has 5 lamps, each with an ordinary on-or-off bulb. The number of ways of lighting the room is

(There are five steps in the procedure of lighting the room, consisting of turning either on or off each of the five lamps.)

example 5

A dance class has 10 men and 12 women. How many ways can the dance instructor choose a couple to demonstrate the foxtrot at a charity ball? There are two steps in forming a dance couple; the instructor must choose a woman and then a man (or vice versa). As there are 12 ways to select the woman and 10 ways to select the man, the number of possible dance couples from the class is

Next suppose the instructor may dress the woman in a long evening gown, a mid-length dress, or a miniskirt, and the man in a tuxedo or suit. How many ways can she choose and dress the couple? The four steps now are

• Step 1 - choose a woman: 12 ways

• Step 2 - choose a man: 10 ways

• Step 3 - dress the woman: 3 ways

• Step 4 - dress the man: 2 ways.

Thus the number of possibilities is

example 6

How many different 3-digit even numbers are there? In writing such a number, we have 9 ways of choosing the first digit (the first digit cannot be zero), then 10 ways of choosing the second digit, and finally 5 ways of choosing the third digit (it must be 0, 2, 4, 6, or 8 if the number is even). The product is 9 · 10 · 5 = 450.

example 7

A set has 4 elements. How many subsets does it have? At first glance this problem appears to have little to do with the multiplication principle. However, the procedure of creating a subset can be broken down into a sequence of steps. Let us name the elements of the set a, b, c, and d. The first step is to decide whether or not the element a is to be in our subset; there are two choices - in or out. Likewise, for each of the elements b, c, and d we have the same two choices. Thus the number of ways of creating a subset from the 4 element set is 2 · 2 · 2 · 2 = 16.

Of course this analysis applies just as well to a set with any number of elements. A set with 2 elements has 2 · 2 = 4 subsets, a set with 3 elements has 2 · 2 · 2 = 8 subsets, etc.

This same question might appear in a variety of forms. For example, in how many ways can a hunter with four dogs decide which dogs to take on a hunting trip? As the hunter is just choosing a subset of his four dogs, the number of possibilities is 2 · 2 · 2 · 2 = 16.

As we have seen, the multiplication principle applies to procedures consisting of a number of steps, or tasks, each of them to be carried out. Our next example illustrates a second fundamental principle of counting; this principle applies to procedures where there are a number of tasks, but only one of them is to be carried out.

example 8

Meeting of   the Civics Club

A civics club consists of

• 9 female Democrats

• 5 male Democrats

• 6 female Republicans

• 7 male Republicans

How many ways can the club choose

(a)  a female Democrat and a male Republican to serve on the budget committee?

(b)  a female Democrat or a male Republican to serve as chairperson?

(c)  a female or a Republican to serve as chairperson?

Question (a) is just another application of the multiplication principle, with two tasks to be performed. The first task is to choose a female Democrat, in one of 9 ways, and the second task is to choose a male Republican, in one of 7 ways. The number of ways of performing both these tasks is 9 · 7 = 63.

Question (b) is different from the previous problems in this chapter. Now, instead of performing both of the two tasks, the club is to perform only one or the other of them. There are 9 ways of selecting a female Democrat, and 7 ways of selecting a male Republican, but the club will carry out only one of these two options. To find the number of ways of selecting one chairman, we put the 9 female Democrats together with the 7 male Republicans, to obtain 9 + 7 = 16 possibilities for chairperson. Thus there are 16 ways of choosing a chairperson meeting the specified conditions.

In question (c), again one or the other of two tasks will be performed, but there is an added complication - it is possible to perform both tasks at once. There are 15 ways of selecting a female, and there are 13 ways to choose a Republican. If we put these two types of candidates together, we will be doing some double counting, as the 6 female Republicans will be counted twice. (This phenomenon is discussed also in the chapter on sets.) To compensate for double counting, after adding 15 females to 13 Republicans we subtract the 6 female Republicans counted twice to arrive at 15 + 13 − 6 = 22 candidates for chairperson. Hence there are 22 ways of choosing a female or a Republican from the club.

Questions (b) and (c) of the preceding example have prepared us for our second fundamental principle. When you have a choice of two methods of performing a procedure, then the number of ways of performing the procedure is found by adding the number of ways using the first method and the number of ways using the second method - however, if there is double counting you must subtract for this phenomenon.

Part (a) of the addition principle works also for more than two tasks. If the civics club wishes to choose as chairperson a female Democrat or a male Democrat or a female Republican, the number of ways is 9 + 5 + 6 = 20. Part (a) of the addition principle applies because there is no way any two of the three tasks can be performed at once - consequently when we add the three numbers together we can do no double counting.

Part (b) of the addition principle becomes quite a bit more complicated when there are more than two tasks and some of the tasks can be performed at the same time; in such situations not only double counting but also triple counting (or worse) can occur. We will not study these more complicated problems.

Novices in counting sometimes are confused about which counting principle - multiplication or addition - applies in a given situation. Just remember that “or” goes with addition, while “and” goes with multiplication.

example 9

Angie will draw one card from a standard deck of playing cards. How many ways can she choose

(a)  a king or a queen?

(b)  a king or a black card?

(c)  an even number or a spade?

(d)  a heart, a diamond, or a club?

In (a) there are 4 ways of choosing a king and 4 ways of choosing a queen, and Angie cannot choose both a king and a queen on only one draw. By part (a) of the addition principle, there are 4 + 4 = 8 ways of getting a king or a queen.

In (b), there are 4 ways of choosing a king, 26 ways of choosing a black card, and 2 ways of choosing both a king and a black card on the same draw (the king of spades and the king of clubs). By part (b) of the addition principle, there are 4 + 26 − 2 = 28 ways of choosing a king or a black card. (Adding 4 + 26 counts the 2 black kings twice, so these must be subtracted.)

To work (c), first we count the number of even numbered cards in a deck; in each of the four suits we have 2, 4, 6, 8, and 10 - thus there are 4 · 5 = 20 cards with even numbers. The number of spades is 13, and there are 5 cards that are both even numbered and a spade. Again by part (b) of the addition principle, the number of cards that are even or a spade is 20 + 13 − 5 = 28.

In (d) there are three tasks, but Angie cannot perform any two of them at the same time; thus part (a) of the addition principle applies. There are 13 hearts, 13 diamonds, and 13 clubs, so there are 13 + 13 + 13 = 39 ways of choosing a card of one of these three suits.

example 10

The state of California makes license plates with 3 letters followed by 3 numbers, and also plates with 3 numbers followed by 3 letters. How many different license plates are possible in California?

Here we will use both the multiplication principle and the addition principle in the same problem. In making a single California license plate one of two tasks is performed. One task is making a plate with 3 letters followed by 3 numbers, which can be done in

ways. Alternatively, the second task is making a plate with 3 numbers followed by 3 letters, which can be done in

ways. The number of possible license plates is just the number of ways of performing one or the other of the two tasks. Since not both tasks can be performed in making only one plate, the number of possible license plates is the sum

EXERCISES 2A

1. A family consists of a mother, a father, 3 girl children and 5 boy children. How many ways can the family choose
   1. one girl to wash the dishes and one boy to dry the dishes?
   2. a boy, a girl, and a parent to go grocery shopping?
   3. one child and one parent to sweep the garage?
   4. a father or a girl to take out the trash?
   5. a female or a child to wash the car?
   
   
2. King's restaurant has a breakfast special. For $3.95 you may order bacon or ham as your meat, then you have a choice of scrambled, fried, or poached eggs, you may next add rice, toast, or hash browns, and finally you may opt for orange, grape, apple, or pineapple juice. If Leilani is famished and takes advantage of every option, in how many ways can she order breakfast?
   
   
3. Frank will take three courses next semester. He will select a history course from 3 offerings, a biology course from 2 offerings, and an English course from 5 offerings. In how many ways can he choose his courses?
   
   
4. How many possible 5-number zip codes are there?
   
   
5. U. S. radio stations have 4 call letters, the first of which must be K or W. How many different sequences of call letters are there?
   
   

Reginald is taking a geology quiz. How many ways can he answer all the questions on the quiz if the test has 5 true-false questions? the test has 5 multiple-choice questions, each having 4 choices? the test has 3 true-false questions, followed by 2 multiple-choice questions having 4 choices each? the test has 2 true-false questions, 2 multiple-choice questions having 4 choices, and 1 multiple-choice questions having 5 choices?

7. Betsy will fly from Honolulu to LA, spend a day and fly to Denver, then spend two days and fly to New York. She has a choice of 7 airlines from Honolulu to LA, 4 airlines from LA to Denver, and 5 airlines from Denver to New York. How many ways can she choose the airlines for her three flights?
   
   
8. A room has 4 lamps with ordinary on-or-off bulbs, and 2 lamps with 3-way bulbs (low, medium, high, or off). In how many ways can the room be lighted?
   
   

Larry, Moe, and Curly are buying ice cream cones in a store where there are 10 choices for flavors. How many different ways can the three decide on flavors, if each orders one scoop of ice cream? each orders two scoops of ice cream, and the top scoop may be of a different flavor from the bottom scoop? Larry orders one scoop, Moe two scoops, and Curly three scoops? each orders one scoop, but the cones come in two flavors?

10. How many different 4-digit numbers are there
    1. that are odd,
    2. that are odd and larger than 3000,
    3. that have only odd digits,
    4. that have only even digits.
    
    
11. A father with 7 sons will clean up his yard. His wife suggests he ask his sons for help. How many ways can the father decide which sons will help him clean the yard? (He may ask all his sons, none of them, or only some of them.)
    
    
12. Three people enter an elevator on the ground floor, in a building with seven upper floors. How many ways can the three people choose upper floors from where to exit the elevator? (E.g., one way is for Al and Bev to get off at floor 3, and Carl at floor 6.)
    
    
13. A young recently married couple hopes to have 6 children. One possible sequence of genders of their 6 children is
    
    boy  ,  girl  ,  girl  ,  boy  ,  girl  ,  boy .
    How many different sequences of genders of six children are possible?
    
    
14. In taking one card from a deck of 52, how many ways can you choose

    a.  a face card or a six?		d.  a face card or a red card?
    b.  a heart or a queen?		e.  a two, a five, or a face card?
    c.  a spade or a black card?		f.  a red card or an even number?

    
    

Next semester there are 3 physics courses Faye can take, 4 biology courses, 5 history courses, and 6 English courses. How many ways can Faye choose a physics course and a biology course? a physics course or a biology course? a biology course and a history course and an English course? a biology course or a history course or an English course? a physics course or a biology course, and a history course or an English course? a physics course and a biology course, or a history course and an English course?

16. A college acting class has 6 junior women, 8 junior men, 5 senior women, and 4 senior men. How many ways can the teacher select
    1. a male to perform a soliloquy from Hamlet?
    2. a woman or a senior man to tap dance?
    3. a junior or a woman to sing a Broadway musical piece?
    4. a senior couple to do a scene from Romeo and Juliet?
    5. a senior couple or a junior couple to do a scene from Romeo and Juliet?
    6. a senior or a woman to call the roll, and a junior man to sweep the stage?